If you enjoy these games, you will certainly enjoy the games at:

Highly recommended!

 

 

PRIVACY

 

We guarantee that we will never sell, rent, give or distribute your personal information (name, address, email, credit card, etc) to anyone else.

 

We, too, hate spammers and mad-dog marketeers!

 

Latin Squares Tutorial

Latin Squares is a little less straight-forward than some of my other games, in terms of the deductions (spatial relationships) that must be spotted. On this page, you'll find a sampling of the types of deductions and situations that you'll find (and find useful) within the game.

In the diagrams on this page, I've added letters to the rows and numbers to the columns as identifiers.

Remember, the rule of the game: There must be one and only one copy of each letter in each ROW, COLUMN and TILE of the puzzle. This places major constraints on the placements of the letters. In this tutorial, I won't talk about deductions involving clues, as they tend to be fairly simple and straight-forward (and fairly well explained by the game's Hint explanations). Instead, I'll focus on the deductions that result from the "spatial constraints."

NOTE: while many of the following explanations follow through a large part of the deduction process of a single puzzle, some steps are skipped, and sometimes I'll "drop back" and take an alternate route in order to illustrate a particular situation. Consider each deduction below as a separate problem/situation rather than a connected string or sequence. Also, many of the following deductions will be explained only in terms of either rows or columns, but not both, for the sake of brevity. Spatial deductions that apply to rows always apply, after proper "rotation", to columns, and vice versa. (Or is that versa vice?)

Deduction #1

 


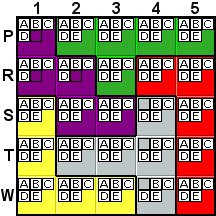Look at the purple tile (top-left W-shape in puzzle). The only remaining locations that contain the letter E as a possibility are S2 and S3. These are both in the same row, and since every tile must contain an E, one of S2 or S3 must be an E. It doesn't matter which one of them is the E, either one will then also be the E that's in row S. Therefore, there can't be any other E's in row S. So, the E's that are shown as possibilities in S1, S4, and S5 can be removed. As another way of looking at this, imagine that one of the E's located in S1, S4, or S5 was the E in row S. That would force the removal of the E possibilities in S2 and S3, leaving the purple tile with NO remaining E possibilities, which would violate the rule of the game.

Also, T2 & T3 contain the last A possibilities in the gray tile (the sidewise-T in the bottom center), so the A's can be removed from T1 and T5.

This deduction is explained in the hint as "X can't be here as it has to be in this row in another tile." (Where X is a letter, E or A in the two examples above.) This same type of deduction applies in the same way to columns.

 Deduction #2

 


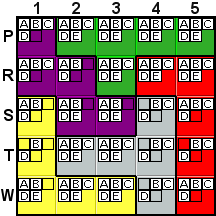T2 and T3 contain the last two A and the last two E possibilities in the gray tile. Since the A has to be located in one of those two cells and the E has to be located in one of those two cells, those two cells can only be A and E. So, the B, C, and D possibilities can be removed from T2 and T3. This is explained in the hint as "These can't be here as it's one of only 2 locations in this row for 2 other letters." Another way of looking at it is that B, C, and D are the only possibilities at 3 locations: S4, T4, and W4. One of those three must be located at each of those three locations in order for there to be any letter at those three locations. That means that those three letters can not be located anywhere else within the tile, specifically at T2 and T3.

This same deduction applies to column 4, where A and E are only possible in P4 and R4, so B, C, and D can't be in those two locations.

 Deduction #3

 
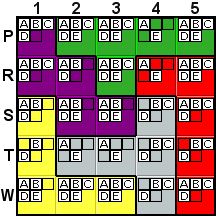This one's a little trickier. R3 can not be A or E. If it were A, for example, then that would the A in the green tile (which would force the removal of the A from all other green cells, including P4), and it would also be the A in the R row, forcing the removal of A from all other cells in the row, including R4. This would remove all A's from column 4, which would violate the rules of the game. This is an example of a deduction which is simple enough for most human players to be able to see, but which the game program would use a What-If to deduce.

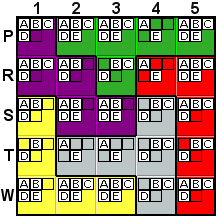
 Deduction #4


Look at the green tile. You will notice that all of the green cells are in the same row, P, except for one, R3. Further, that the green cells take up all of the cells in row P except for one, P1. Whatever letter is located in R3 can not be in any of the other green cells, which leaves only P1 as the location in row P for whatever letter is located in R3. In other words, in this kind of situation, you instantly know that P1 and R3 must contain the same letter. So, any time one of them contains a possibility that is not in the other, that possibility can be removed. In this example, the A can be removed from P1. Another way of looking at this is that all green A's are in row P, so no matter where the green A is located, it will be in row P, so A cannot be located in any other tile in row P, specifically P1. This is explained in the hint as "A can't be here as it has to be in this row in another tile."

A similar relationship exists between R4 and P5. All of the red cells except for R4 are in column 5, so whatever letter is located at R4 must also be located at P5. So, B, C, and D can be removed from P5.

 Deduction #5
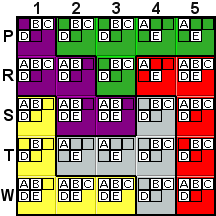W1 must be E, as it's the last cell in column 1 with E as a possibility. This is explained in the hint as "Last place in column for E."

 Deduction #6
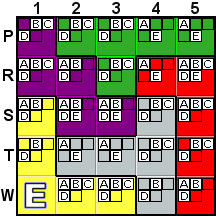Here's another deduction that you can make fairly easily through simple observaton, but which the program will need to use a What-If to deduce. The green tile is contained entirely within rows P and R, so all of its C possibilties are within those two rows. The purple tile exists within rows P, R, and S, but it has no C possibilities remaining in row S. So, both the green and the purple C's must be in rows P and R. Either the green C is in row P and the purple C is in row R, or vice versa. Either way, there's no room left in rows P and R for a C in any other tiles. Therefore, we can remove the red C from R5.

 Deduction #7


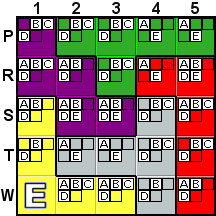
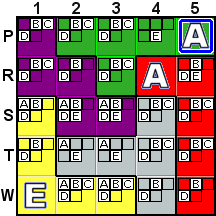
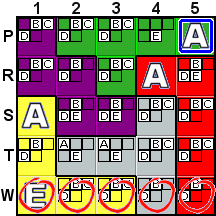Here we'll step through a "What-If" type of deduction. As mentioned in Deduction #4, R4 and P5 must contain the same letter. Let's suppose (what-if) that P5 A (by depressing the What-If button and then left-clicking on the A). That means that R4 is also A (as shown in the second picture).

Now, in the second picture, you'll notice that the placement of the A in R4 has forced the removal of the A possibility from R1, leaving S1 as the only possible location for A in column 1.

Placing the A in S1 results in the situation shown in the third picture, where there are no A possibilities left in row W. This obviously violates the rule of the game, so our initial supposition (the A in P5) can not be right. Therefore, since P5 cannot be A, it must be E. So, we would undo all of the deductions we'd made (by unclicking the What-If button), and then removing the A from P5.

 Deduction #8
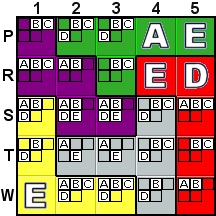S2 and S3 contain the last two possibilities for both D and E, so those two locations have to be those two letters and can't be A or B. This deduction is very similar to Deduction #2, but practice makes perfect...

 Deduction #9
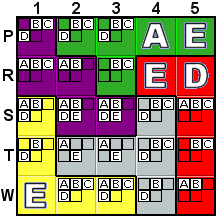Similar to Deduction #4, but a bit more complex to see, S1 and R2 must contain the same letter. You will notice that S1 is in the same row or the same column as every other purple cell except for R2. That means that no matter what letter is placed in S1, that letter will be removed as a possibility from every cell of the purple tile except for R2, forcing R2 to contain the same letter as S1. This means that the D can be removed from S1, since it's not possible in R2. In other words, placing D at S1 would remove all D possibilities from the purple tile, so that can't be. This is another situation that the program would use a What-If to spot, but that can be easily seen by the human eye.

 Deduction #10
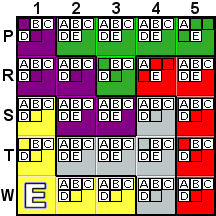In this situation, the A can be removed from S4 and W4, because the only remaining A's in row T are in the gray tile, so no A's can be allowed in any other rows of the gray tile or they would cause the removal of all remaining A's from row T.